Performance analysis for wireless-powered IoT networks with hybrid non-orthogonal multiple access
Abstract
Aim: In this paper, we study a wireless-powered Internet of Things (IoT) network, where a hybrid access point (HAP) charges IoT devices with wireless energy transfer technology (WET) and collects their data by wireless information transfer (WIT).
Methods: To improve spectral efficiency, we propose a hybrid non-orthogonal multiple access (NOMA)-based transmission scheme. On the one hand, NOMA technology is applied for WIT. On the other hand, when some devices transmit data, the HAP can simultaneously charge the other devices, namely concurrent WET and WIT, such that the other devices can harvest more energy to achieve a better rate with some rate loss of these devices due to interference. %During the transmission of some devices, the WET is simultaneously conducted, such that other devices can harvest more energy to achieve a better rate with a rate loss of these devices due to the interference. How to divide devices into the interference and non-interference groups, namely device grouping, and how to pair devices, e.g., device pairing, becomes critical issues in terms of the achieved network throughput and fairness.
Results: We first formulate the network throughput maximization problem by optimizing the pairing and grouping policies. To simplify the analysis, we then investigate two specific hybrid NOMA-based transmission schemes. In the former, all devices are firstly paired based on the max-min criterion, where the "best" device is paired with the "worst" one, and then grouped in either ascending or descending order; this is referred to as the first-pairing-then-grouping (FPTG) scheme. In the latter, devices are first grouped and then paired; this is referred to as the first-grouping-then-pairing (FGTP) scheme. By applying the order statistics theory, we theoretically analyze the achieved network throughput and derive the corresponding pairing and grouping policies. Furthermore, we study the max-min fairness of the proposed hybrid NOMA-based scheme.
Conclusion: Simulation results validate the significant improvement of the proposed hybrid NOMA-based scheme in terms of network throughput and fairness.
Keywords
INTRODUCTION
Radio frequency (RF)-based energy harvesting technology is an emerging potential solution for providing continuous and sustainable energy supply to wireless devices over the air[1, 2]. By employing it, a hybrid access point (HAP) charges devices in the downlink via wireless energy transfer (WET) and then collects data information from devices in the uplink, namely wireless information transfer (WIT). This framework is referred to as wireless-powered communication networks (WPCNs), and it is an emerging framework for sustainable wireless networking which has attracted much research attention in the past years.
Recently, many research works have investigated WPCNs [3, 4, 5, 6, 7, 8], where the energy harvested from the RF energy source is used for information transmission of wireless devices. In[3], the key network architectures and technologies to build efficient WPCNs are summarized and some challenging research directions are pointed out. In[4], all devices first harvest radio energy broadcasted by the HAP in the downlink (DL), and then send their information to the HAP via the time division multiple access (TDMA) manner in the uplink (UL). The achieved network throughput of a WPCN is maximized in[5] subject to the energy causality, time duration, and quality-of-service (QoS) constraints, where the time allocated to WET and WIT is optimized. These works validate that WPCNs could significantly increase the network throughput and present a valuable opportunity to address the fundamental energy scarcity issue of wireless networks.
Non-orthogonal multiple access (NOMA) is an emerging and effective method to improve spectral efficiency and connectivity[9, 10, 11]. In[12], green transportation is introduced, the advantages of using backscatter communication and NOMA in the automotive industry 5.0 are discussed, and a multi-cell optimization framework is proposed to maximize the energy efficiency of a backscatter-enabled NOMA vehicle network. In[13], a joint NOMA optimization framework for small cell networks (SCNET) is proposed by exploiting the concept of multi-objective problems. In particular, the transmit power of the base station (BS) in each small cell is simultaneously optimized to maximize the total capacity and total energy efficiency (EE) of the SCNET. To maximize the network throughput of a WPCN, the NOMA transmission scheme is exploited in[9], where the transmit power of the HAP and the time allocation for WET and WIT are jointly optimized. In[10], two different decoding schemes with/without successive interference cancellation are proposed to maximize network throughput by optimizing the time and power allocation. The benefit of NOMA scheme is validated in[11] concerning network throughput, fairness, and energy efficiency.
In[14], half-duplex and asynchronous downlink–uplink transmission are considered. The WET time, transmission power of devices, and decoding order are jointly optimized in[15] for a WPCN with NOMA.
Instead of network throughput, the network fairness issue of wireless-powered communication network is studied in[16, 17, 18]. In[16], it is shown that non-orthogonal access using a successive interference canceller (SIC) can significantly improve user fairness by increasing the throughput of cell edge users compared to orthogonal access. In[17], the fairness of uplink non-orthogonal multiple access (NOMA) and orthogonal multiple access (OMA) schemes are compared, and a fairness metric based on Jain's index is proposed to measure the asymmetry of multi-user channels. The single-input single-output (SISO) NOMA system is studied in[19]. The max–min power allocation problem for maximizing the minimum achievable user rate in clustered multiple-input multiple-output (MIMO) NOMA systems is studied in[18]. The authors of[20] designed power allocation algorithms to achieve fairness in NOMA-based cognitive radio (CR) transmissions for secondary users (SUS). However, to the best of our knowledge, most of the existing works in the literature investigate non-orthogonal information transmission, while how to explore the non-orthogonal transmission between WET and WIT as well as between WIT and WIT has not been thoroughly studied yet, which is the inspiration for this paper. In our previous work[21], a fairness-aware NOMA-based scheduling scheme is proposed for a wireless-powered IoT network, where the NOMA for concurrent WET and WIT is exploited, and the NOMA-based WIT is not taken into consideration.
In this paper, we propose a hybrid NOMA-based transmission scheme for wireless-powered IoT networks, in which NOMA for both simultaneous WET and WIT and simultaneous WIT of devices are jointly explored. To realize non-orthogonal WET and WIT, all devices are divided into two groups, namely the interference group and the non-interference group. Non-orthogonal WET and WIT are conducted during the transmission of devices in the former group, such that the WIT of these devices suffers the interference caused by simultaneous transmission. Thus, the device grouping policy becomes a significant issue in maximizing the network throughput and achieving network fairness. Meanwhile, to realize non-orthogonal WIT of devices, conventional NOMA technology is deployed, and the device pairing policy plays an important role. On this basis, we study the achieved throughput under two specific hybrid NOMA-based schemes, namely the first-pairing-then-grouping (FPTG) and first-grouping-then-pairing (FGTP) schemes. Devices are firstly paired based on their channel qualities, and then grouped in the FPTG policy, and vice versa in the FGTP policy. To analyze the achieved performance, we apply order statistics theory, and then optimal pairing and grouping are determined. Subsequently, we analyze the max–min fairness of the hybrid NOMA scheduling scheme by applying the FPTG and FGTP schemes. Devices are transmitted in the uplink in a non-orthogonal way, and the decoding order at the receiver determines the minimum rate of each pair of devices. We maximize the minimum rate of each pair of devices by adjusting the grouping and pairing devices to achieve maximum–minimum fairness. By simulation results, it is validated that significant network throughput gain and fairness are realized by the hybrid NOMA-based scheme.
SYSTEM MODEL AND PROBLEM FORMULATION
System model
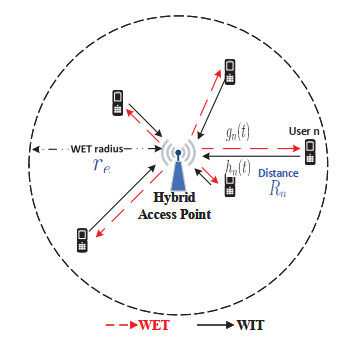
In this paper, we study a WPCN, as illustrated in Figure 1, where
Block fading channels are considered, which means the channel remains constant in a unit of time but varies in different time blocks. Suppose
Meanwhile, the maximum transmit power at the HAP is
Hybrid NOMA transmission scheme
In a WPCN, devices far away from the HAP usually harvest less energy than those close to the HAP, leading to a lower transmission rate. Thus, it is necessary to improve the performance of remote devices with relatively poor channel quality. An alternative method is to supply more energy to devices by a longer WET time while keeping the same information transmission time. To achieve this, we can explore concurrent WET and WIT, namely non-orthogonal energy and information transmission. This is because the energy and information signals are delivered by the HAP and devices, respectively. Note that the energy signal is regarded as an interfering signal that affects the information transmission of IoT devices. Meanwhile, NOMA technology can effectively improve the spectral efficiency and connectivity by allowing concurrent information transmission of multiple devices, such that we incorporate NOMA for WIT into a wireless-powered IoT network. To this end, we propose a hybrid NOMA transmission scheme for a WPCN, in which NOMA for both WIT and concurrent WET and WIT is exploited.
Notations and definitions
| Notation | Definition |
| Number of IoT devices | |
| The communication coverage of HAP | |
| Charging and transmission distance between device | |
| Path loss exponent | |
| Reference distance and reference path loss | |
| Small-scale fading of WET and WIT channels | |
| Maximum transmit power of the PS | |
| Transmission time of WET and WIT slot of device | |
| m | Number of devices in |
| Whether devices | |
| group of device | |
| Transmit power of the PS in slot | |
| Harvested energy of device | |
| Signals transmitted by the HAP and devices | |
| The received signal at the HAP | |
| Noise of device | |
| Energy conversion efficiency, and power of noise | |
| SNR and sum rate of paired devices | |
| pdf and CDF of distance from HAP to device | |
| Sum rate of | |
| The pdf of |
An example of time block structure is presented in Figure 2. The dedicated WET time is denoted as
According to the hybrid NOMA transmission scheme, all devices are divided into two groups, i.e., the interference group of
In the dedicated WET slot, only the HAP transmits energy to charge all devices, such that the amount of energy harvested by device
where
In the WIT slot, according to the NOMA manner, two devices can simultaneously transmit information to the HAP. Define a binary variable
Note that, when
When devices
where
Based on the hybrid NOMA transmission scheme, the total WET times for devices in the interference and non-interference groups are
Given the transmission time
When devices
where
Thus, the achievable sum rate of paired devices
The practical sum rate of devices
THROUGHPUT ANALYSIS OF HYBRID NOMA TRANSMISSION SCHEME
Problem formulation
In this paper, we focus on the network throughput under the hybrid NOMA transmission scheme by optimizing the device grouping and pairing policies. Thus, we can formulate the following network throughput maximization (NTM) problem
In the above problem, the first four constraints are the limitation of device pairing policy concerning the NOMA transmission for WIT, which means that a device can be paired with only one other device except itself. Constraint C5 indicates that devices
The formulated optimization problem in Equation Equation(10) is an integer nonlinear programming problem, which is difficult to solve. To reduce the complexity, we investigate the achieved performance of two specific hybrid NOMA transmission schemes. In the former, devices are firstly paired based on their channel qualities, and then the device grouping is decided. In the latter, the device grouping policy is given based on their channel qualities, and then the device pairing policy is determined.
First-pairing-then-grouping scheme
In this subsection, the device pairing policy is first determined based on channel qualities, and then the devices are grouped; this is referred to as the first-pairing-then-grouping (FPTG) policy. Concerning the device pairing policy, we first need to sort all devices in descending order by their channel gains, and then pair the ordered devices based on the max–min pairing policy, which is best to maximize throughput. In the max–min policy, the first ordered device is paired with the
Then, for the device grouping policy, the basic idea is to allow
To achieve this, we first need to analyze the achievable rate
where
Proposition 1Let
where
According to Proposition1, we can calculate the achievable rate for each pair of ordered devices. We suppose that IoT devices are randomly deployed around a HAP with radius
where
Thus, the achievable sum rate of the pair of
Similarly, the achievable sum rate of ordered devices
In the following part, we consider two cases.
Case I: The first
Accordingly, the network throughput maximization problem is to determine the optimal
To solve this, we study the effect of
where
According to Equation (18) and Equation (19), it can be concluded that the throughput gain
Case II: The later
In this case, when
First-grouping-then-pairing scheme
In this subsection, the device grouping policy is first determined based on channel qualities, and then the devices are paired; this is referred to as the first-grouping-then-pairing (FGTP) policy. We first sort all devices in descending order based on their channel gains. Concerning the grouping policy, we consider two cases: Case I, the
Case I: The
Case II: The
To this end, the problem is to determine the number of devices in the interference group, namely
FAIRNESS ANALYSIS OF THE HYBRID NOMA TRANSMISSION SCHEME
In WPCNs, devices far away from the HAP harvest less energy compared to devices close to the HAP, but they need to transmit at higher power in order to achieve a specific rate, which can lead to a double near–far effect. The double near–far effect causes serious fairness issues in wireless-powered IoT networks. Therefore, in this section, we analyze the fairness of the hybrid NOMA transmission scheme by determining the device grouping and pairing policies. Here, we focus on the max–min fairness to unveil the effect of the double near–far problem in wireless-powered IoT networks.
In the WIT phase, device
At the HAP, the messages of two users are decoded using successive interference cancellation (SIC). To achieve max–min fairness, the decoding order of the HAP for users
In the first case, the HAP first decodes the signal sent by device
In the second case, HAP decodes the signals sent by
After calculation, the minimum rate achievable for each pair of devices
Thus, we can express this max–min fairness problem as
As in the problem in Equation (10), to solve the problem in Equation (26), we investigate the fairness performance under two specific hybrid NOMA transmission schemes, namely FPTG and FGTP.
First-pairing-then-grouping scheme
In this subsection, the FPTG policy is considered. Firstly, all devices are required to be sorted according to their channel gains from highest to lowest, and the sorted devices are paired according to the max–min pairing policy, i.e., the
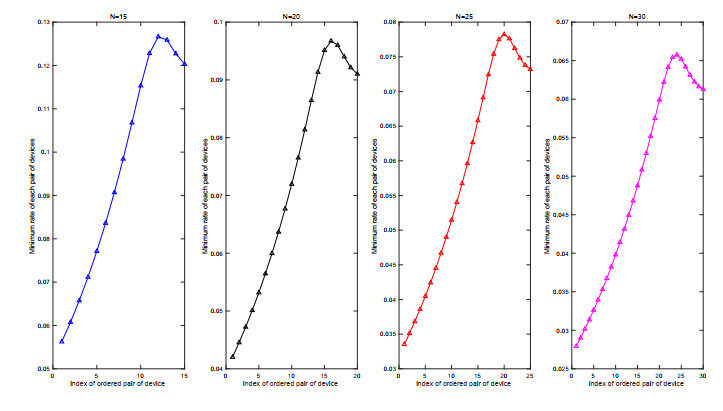
The first step is to decide the devices to be divided in the interference group. Based on the basic idea of improving network fairness, the device with the higher minimum rate should be assigned to the interference group to suffer from WET interference, and the rate of the worse performing device in the non-interference group is improved at the expense of the rate of the better device. Therefore it is important to determine which device pairs have higher minimum rates. Figure 3 compares the minimum rates of devices performing non-orthogonal transmission in descending order according to channel conditions and performing max–min pairing for different numbers of device pairs
To determine the optimal
The minimum achievable rate for the paired ordered devices
According to proposition1, the achievable minimum rate of the pair of
Simulation parameters
| Simulation parameter | Value |
| 2N | 40 |
| 20 m | |
| 0.1 | |
| 1 m | |
| 3 | |
| 1 | |
| Interference channel | |
| 1/N+1 |
The achievable minimum rate of the pair of
where
First-grouping-then-pairing scheme
In this subsection, we consider the FGTP strategy. We first sort all devices in descending order based on channel gain. Then, the
PERFORMANCE EVALUATION
In this section, we evaluate the performance of our proposed hybrid NOMA-based transmission scheme. We set the number of users as
Throughput of the hybrid NOMA scheme
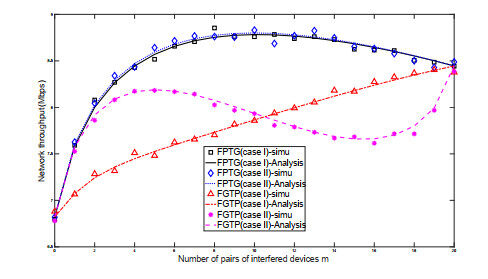
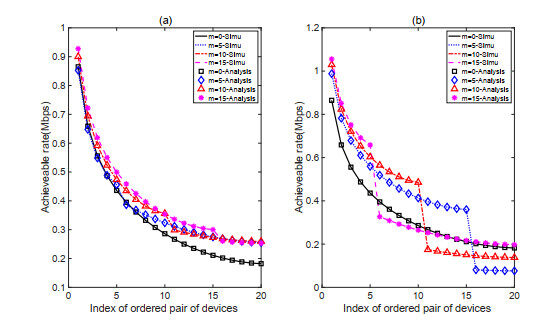
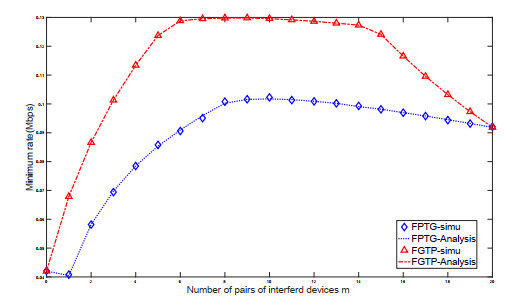
In Figure 4, we compare the throughput of the four policies using analytical and simulation methods, respectively. The simulation results follow the same trend as the computed results, and they fluctuate above and below the theoretical results.Notice that, when
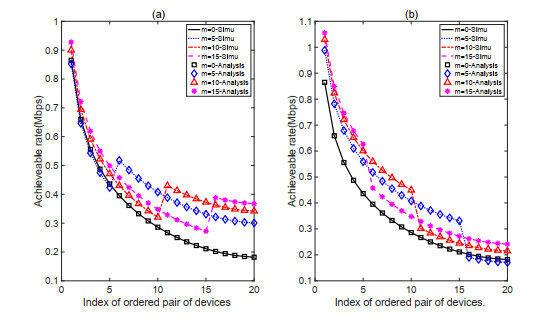
Figure 5 and Figure 6 present the rate of each device for the FPTG and FGTP schemes under two cases, respectively. If
Figure 5(a) and Figure 6(a) show the case where
Figure 5(b) and Figure 6(b) show the situation where the
In Figure 6(a), the rate of the devices in the non-interference group remains basically the same at different
Fairness of hybrid NOMA scheme
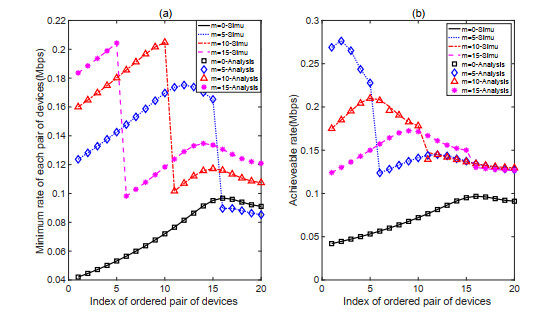
We then evaluate the max–min fairness of the proposed hybrid NOMA transmission scheme under two strategies. The achievable minimum rate of each pair of ordered devices under each strategy is shown in Figure 7. The simulation results are consistent with our analysis. When
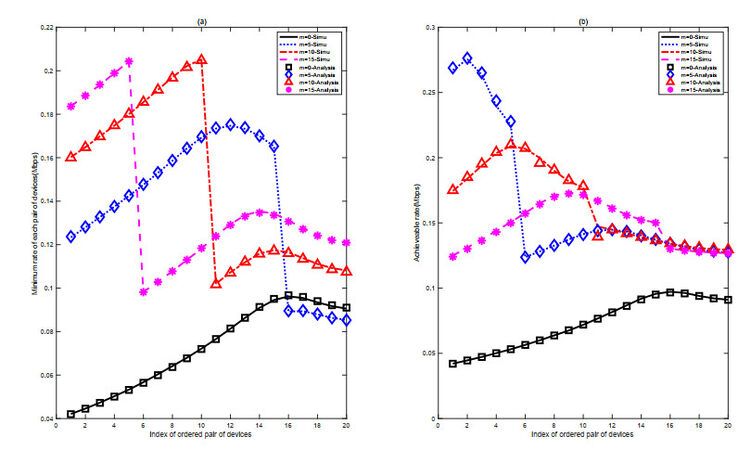
In Figure 8, we show the minimum rate of all IoT devices under different number
For the FGTP strategy shown in Figure 8(b), the minimum rate of devices in the interference group
Figure 9 compares the minimum rates of
CONCLUSION
In this paper, we propose a hybrid NOMA-based transmission scheme to maximize the network throughput of a wireless-powered IoT network, in which the NOMA for both simultaneous WET and WIT and simultaneous WIT of devices are jointly explored. We apply the order statistics theory to analyze the optimal device pairing and grouping policies of the hybrid NOMA scheme in terms of network throughput and fairness, respectively. Simulation results are consistent with the analysis and verify the significant gain of the proposed hybrid NOMA-based transmission scheme. In the future, this work could be extended to multi-cell wireless-powered IoT networks with mobility.
DECLARATION
Acknowledgments
We thank the editors and reviews for the constructive comments on the manuscript, which help us to improve the quality of this work.
Authors' contributions
Made substantial contributions to conception and design of the study and performed data analysis and interpretation: Qi HW, Zhang H
Writing of the original draft preparation: Qi HW
Revision of the manuscript: Peng YS, Zhang H
All authors have read and agreed to the published version of the manuscript.
Availability of data and materials
Not applicable.
Financial support and sponsorship
This work was supported by the National Natural Science Foundation of China under grant No. 61901180, Natural Science Foundation of Guangdong Province under grant No. 2019A1515011940, No. 2022A1515010111, Science and Technology Project of Guangzhou under grant No. 202002030353, and Basic and Applied Basic Research Project of Guangzhou under grant No. 202201010574.
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2022.
REFERENCES
1. Lu X, Ping W, Niyato D, Dong IK, Zhu H. Wireless networks with RF energy harvesting: a contemporary survey. IEEE Commun Sur & Tut 2015;17:757-89.
2. Clerckx B, Zhang R, Schober R, et al. Fundamentals of wireless information and power transfer: from RF energy harvester models to signal and system designs. IEEE J Sel Areas Commun 2018;37:4-33.
3. Bi S, Zeng Y, Zhang R. Wireless powered communication networks: an overview. IEEE Wireless Commun 2016;23:10-8.
4. Ju H, Zhang R. Throughput maximization in wireless powered communication networks. IEEE Trans Wireless Commun 2013;13:418-28.
5. Zhao F, Wei L, Chen H. Optimal Time Allocation for Wireless Information and Power Transfer in Wireless Powered Communication Systems. IEEE Trans Veh Technol 2016;65:1830-5.
6. Chen J, Zhang L, Liang YC, Kang X, Zhang R. Resource allocation for wireless-powered IoT networks with short packet communication. IEEE Trans Wireless Commun 2019;18:1447-61.
7. Yu Z, Chi K, Hu P, Zhu YH, Liu X. Energy provision minimization in wireless powered communication networks with node throughput requirement. IEEE Trans Veh Technol 2019;68:7057-70.
8. Chen Z, Chi K, Zheng K, Dai G, Shao Q. Minimization of transmission completion time in UAV-enabled wireless powered communication networks. IEEE Internet of Things Journal 2019;7:1245-59.
9. Chingoska H, Hadzi-Velkov Z, Nikoloska I, Zlatanov N. Resource allocation in wireless powered communication networks with non-orthogonal multiple access. IEEE Wireless Commun Lett 2016;5:684-7.
10. Abd-Elmagid MA, Biason A, Elbatt T, Seddik KG, Zorzi M. Non-orthogonal multiple access schemes in wireless powered communication networks. In: 2017 IEEE International Conference on Communications (ICC); 2017.
11. Diamantoulakis PD, Pappi KN, Ding Z, Karagiannidis GK. Wireless-powered communications with non-orthogonal multiple access. IEEE Trans Wireless Commun 2016;15:8422-36.
12. Khan WU, Ihsan A, Nguyen TN, Javed MA, Ali Z. NOMA-enabled backscatter communications for green transportation in automotive-industry 5.0. IEEE Trans Ind Inf 2022; doi: 10.1109/TⅡ.2022.3161029.
13. Khan WU, Jameel F, Li X, Bilal M, Tsiftsis TA. Joint spectrum and energy optimization of noma-enabled small-cell networks with QoS guarantee. IEEE Trans Veh Technol 2021;70:8337-42.
14. Zewde TA, Gursoy MC. NOMA-based energy-efficient wireless powered communications. IEEE Trans Green Commun and Networking 2018;2:679-92.
15. Chen Z, Chi K, Zheng K, Li Y, Liu X. Common throughput maximization in wireless powered communication networks with non-orthogonal multiple access. IEEE Trans Veh Technol 2020;69:7692-706.
16. Takeda T, Higuchi K. Enhanced user fairness using non-orthogonal access with SIC in cellular uplink. In: 2011 IEEE Vehicular Technology Conference (VTC Fall); 2011. pp. 1-5.
17. Wei Z, Guo J, Ng DWK, Yuan J. Fairness comparison of uplink NOMA and OMA. In: 2017 IEEE 85th Vehicular Technology Conference (VTC Spring); 2017. pp. 1-6.
18. Liu Y, Elkashlan M, Ding Z, Karagiannidis GK. Fairness of user clustering in MIMO non-orthogonal multiple access systems. IEEE Commun Lett 2016;20:1465-68.
19. Timotheou S, Krikidis I. Fairness for non-orthogonal multiple access in 5G systems. IEEE Signal Process Lett 2015;22:1647-51.
20. Ali Z, Khan WU, Sidhu G, Nimmi K, Bilal M. Fair power allocation in cooperative cognitive systems under NOMA transmission for future IoT networks. ALEX ENG J 2022;61:575-83.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Qi H, Peng Y, Zhang H. Performance analysis for wireless-powered IoT networks with hybrid non-orthogonal multiple access. J Smart Environ Green Comput 2022;2:105-25. http://dx.doi.org/10.20517/jsegc.2022.04
AMA Style
Qi H, Peng Y, Zhang H. Performance analysis for wireless-powered IoT networks with hybrid non-orthogonal multiple access. Journal of Smart Environments and Green Computing. 2022; 2(3): 105-25. http://dx.doi.org/10.20517/jsegc.2022.04
Chicago/Turabian Style
Qi, Huiwen, Yingsheng Peng, Han Zhang. 2022. "Performance analysis for wireless-powered IoT networks with hybrid non-orthogonal multiple access" Journal of Smart Environments and Green Computing. 2, no.3: 105-25. http://dx.doi.org/10.20517/jsegc.2022.04
ACS Style
Qi, H.; Peng Y.; Zhang H. Performance analysis for wireless-powered IoT networks with hybrid non-orthogonal multiple access. . J. Smart. Environ. Green. Comput. 2022, 2, 105-25. http://dx.doi.org/10.20517/jsegc.2022.04
About This Article
Copyright
Data & Comments
Data

 Cite This Article 11 clicks
Cite This Article 11 clicks












Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.