Solar powered UAV charging strategy design by machine learning
Abstract
Aim: The rapid growth in the number of ground users over recent years has introduced the issues for a base station of providing more reliable connectivity and guaranteeing the reasonable quality of service (QoS). Thanks to the unique features of unmanned aerial vehicles (UAVs), such as flexibility in deployment, large coverage range and lower cost, UAVs can help the base station to provide wireless connectivity to the ground users, e.g., in rural and remote areas. As the energy limitation is the main concern for UAVs, the motivation is to provide uninterrupted connection to ground users in the next generation wireless networks using solar powered UAV-assisted air networks.
Methods: The research uses global horizontal irradiance (GHI) data from the National Renewable Energy Laboratory, small cell power ratings for communication, and UAV parameters. In addition, the TensorFlow library and Python programming language were also used to develop machine learning models and simulate the UAV flying time.
Results: In this paper, we develop a novel resource management system for UAVs, which consists of an energy harvesting deep learning model to predict the future power harvested from the solar panel and a consumption model which determines user arrival rate. With energy consumption and harvesting predictions, the resource management system adaptively switches the power consumed by a UAV for communication. In addition, based on the future energy availability and user's arrival rate, the resource management system communicates with other UAVs and enables energy coordinating scheduling among multiple UAVs to support user communications. The experiment results demonstrate that by using adaptive energy scheduling among UAVs, the flying time of the UAVs is improved by 40% during nighttime and by 37% when performing energy coordination among multiple UAVs.
Conclusion: In this work, the UAV based communications have been researched. To understand more about UAVs and air segments, some literature review has been done based on previous works. Finally, alteration of the transmission power using several methodologies has been accomplished to increase the flying time of the UAV.
Keywords
INTRODUCTION
In recent years, space air ground integrated networks (SAGIN) are emerging to provide wide area coverage and high throughput to the users [1]. SAGINs consist of three primary layers, namely the space layer (e.g., the satellites used to provide communication to rural and mountain regions), the air segment (e.g., unmanned aerial vehicles (UAVs) used to extend the coverage for communication), and the ground network (e.g., to provide high data rate). By considering the air segment, the UAVs play an important role in providing broadband wireless communication supplementing the terrestrial networks. In contrast to the base stations in the terrestrial networks, the UAVs are less costly and easy to deploy to provide uninterrupted but prompt connection to the users, especially during dangerous and disaster situations. Considering the air segment, the UAVs can be customized to carry radio communication elements and deployed into the air. As they run on battery power, the energy from the battery is quickly consumed, requiring the UAVs to be manually recharged, and the battery-powered UAVs are made to connect with the ground system, which monitors the battery levels and automatically makes the UAVs recharge by landing at the docking stations [2]. The periodic recharging due to the limitation of the battery size of UAVs reduces their flying time. To increase the UAVs flying time for supporting ground communications, the solar powered UAVs are introduced with deploying solar panels and harvesting the solar energy from the sun.
The solar powered UAVs for perpetual flight have been developed in [3], e.g., solar powered UAV has 66 solar cells on the wings. The UAV is designed to propel itself using a single motor to achieve a flying time of 28 hours without any payload on it. The payloads are the radio communication equipment or small base stations (called small cells), which provide mobile and internet services to a localized range. With carrying payloads in the UAVs, the energy is consumed by both UAV and communication equipment, which tends to decrease the flying time compared to [3]. Energy consumption by the UAVs can significantly reduce the staying time and affects the communication with users. In order to improve the flying time and to support the users, the solar powered UAVs should possess a way to monitor the energy in their batteries and to know how optimally they can utilize the harvested power for communication. In [4], a statistic model has been developed for the harvested energy from renewable resources. Based on the developed model, the probability of energy outage in the UAV, the probability of charging time while UAV in air and the probability of signal-to-noise ratio disruption to the users can be determined. However, the above work only estimates the energy outage but does not provide any time series forecasting of solar power and lacks an optimization function to improve the flying time. The statistical and averaging models are quite intuitive to formulate the system using mathematical equations, which helps in extracting the relationship between variables to predict the outcomes. However, the pattern of the dataset is not well captured and apart from solar data, other values like temperature and weather data are not considered. On the other hand, deep learning algorithms can easily identify the pattern in provided dataset by iterating over the dataset several times, and the model can also be trained using weather data, which helps in predicting the future solar power values.
Instead of calculating the charging time using a statistical model, this work uses the solar power dataset and deep learning algorithm to predict the future harvested solar power. We develop an energy optimization algorithm to adaptively switch the power utilization based on the prediction of the amount of power in UAVs by machine learning. We support the future power requirement using the user arrival rate and develop the energy scheduling strategy using multiple UAVs to support the users. To this end, the paper answers the questions of (1) how the system adaptively utilizes the power from batteries based on the number of users in a given range; (2) based on future power requirements, how the energy scheduling using multiple UAV works; and (3) how these two elements help the UAV to stay in the air for a longer duration.
The remainder of the paper is organized as follows. Section II gives a glance at related works. Section III proposes the system model. The problem formulation and proposed algorithm is discussed in Section IV. Section V demonstrates the simulation and testing results, followed by a conclusion in Section VI.
RELATED WORKS
Many exploration works have been done to support the correspondence for ground users in remote and natural calamity regions. In [5], the author expresses that SAGINs are broadly proposed these days, particularly the air networks in SAGINs play a significant role in providing communication support to the ground users. It is because the static terrestrial base stations cannot provide great support to users due to their limited coverage. A larger disaster can make the base station over-burden, and in [6], the author expresses that it is important to construct an emergency network utilizing UAVs to give a high data rate and reliable connectivity to the ground users. A simulation-based SAGINs in [7] discusses controllers that are carried out to enhance the communication elements and to serve effective QoS to the ground users. The previous references have no insights into how the energy is optimized to make the UAVs fly for longer lengths. However, in [8], a mathematical-based approach discusses how the energy efficiency of the air network is expanded utilizing non-linear convex approximation. Aside from the network optimization and convex approximation methods, a compelling technique ought to decide how actually the energy can be utilized from the UAV to satisfy the ground users. To solve this problem, the author in [9] and [10] developed a small-scale UAV with solar panels implanted on the wings to harvest the solar power and accomplished a multi-day flying time.
Meanwhile, research works have been completed in sizing and testing of the solar powered UAVs; in [11] the altitude and the payloads of UAVs are considered as parameters, and their consequences on the UAVs are studied. The outcomes from studies helped with deciding the size, payload and altitude at which the aircraft to fly to collect more solar power and use it for flying. The enhanced design and testing of solar powered UAV in [12] uncovers its maximum endurance and the effectiveness of the solar panel mounted on it.
In [13], the energy coverage performance of the different network systems is analyzed by finding the line of sight probabilities and the impact of the 3D antenna. The simulation has been carried out by implementing different antenna patterns and varying the UAVs' heights. The analysis shows how the energy performance has been improved by changing the antenna pattern, user count, and UAV height. However, the work did not show the increase in flying time based on different heights and ground user count. Also, in [14], the author used a deep Q network to optimize the UAVs' capacity to support the ground users. Although they used solar powered UAVs, they have not included a scheduling mechanism to support future users in the desired UAV range.
Machine learning-based solar powered UAVs are used to increase the flying time of the UAVs; in [15] solar powered UAVs are developed with reinforcement learning agents, so they can change their position adaptively by deciding the solar energy density and other environmental circumstances. The reinforcement learning only helps to place the UAV in the higher solar power regions, and it does not have any feedback mechanism to estimate the flying time and future solar power values. The solar UAV in [16] acts as a bridge between the ground users and the local base station. The users' data is captured and the harvested solar power is utilized to transmit the captured data to the static base station. This method assumes the ground users data count, not an estimate of it. In [17], power distribution and trajectory planning problems are addressed utilizing machine learning in a multi-UAV-based correspondence framework. The system has IoT nodes at different distances; therefore, the trajectory of the UAVs is optimized to collect data from the nodes and send it to the server. Some research works in [18] and [19] solved trajectory optimization and resource allocation problems utilizing the convex approximation method, which accomplishes a high throughput in providing communication to the users. In these works, the solar powered UAVs are not used and the main focus is on collecting data from different locations. Nevertheless, in our contribution, the solar powered UAVs are used to improve the flying time and also provide communication support to ground users in fixed locations.
SYSTEM MODEL
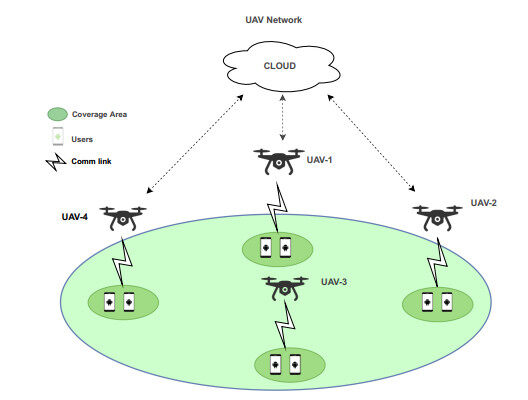
The proposed system model is displayed in Figure 1. The total framework is partitioned into the UAVs and the cloud layer. The cloud layer lives in the UAV network server, which gathers data about solar harvesting power, energy, the arrival rate of ground users in the region, and the location coordinates of the UAVs. Based on this information, the cloud's optimization algorithm conveys the transmission power value and the location coordinates to the UAVs (where it ought to position itself).
By receiving the cloud's parameter values, the UAVs help the ground users. In this work,
Time is divided into
where
A cloud part in the framework, as displayed in Equation (1), concentrates data about appearance of the ground users utilizing the number of dynamic associations inside the small cell range. The cloud decides the distance between the UAVs by Equation (2). The collected solar power and the battery energy of each UAV in the network are gathered by the cloud. Utilizing the gathered information, the cloud runs an optimization algorithm to organize UAVs in the network and support the ground users successfully.
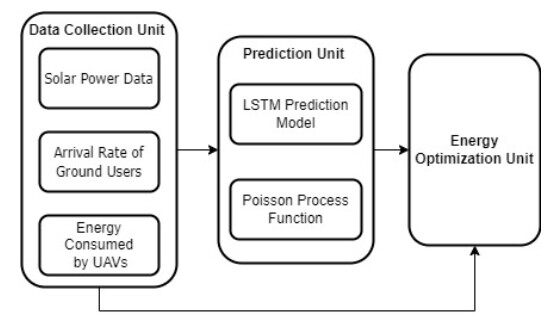
Figure 2 shows the functioning model of the cloud framework. The system is separated into three unique parts, information collection, prediction, and energy optimization unit. In the information collection part, the first block cloud is used for collecting reaped solar-based power values from the UAVs, the subsequent block is used for collecting the data about the number of ground users in the vicinity, and the last one is used for gathering the data about UAVs energy consumption.
A long short-term deep learning model is used for predicting the forthcoming solar power, and the Poisson process is used for determining the average arrival rate of the ground users. Towards the end, two actions are performed when the unit obtains the data. First and foremost, the power value to each UAV is sent based on the user's demands to change the input power from a UAV to a small cell. Secondly, based on the determined distance, predicted users, and future solar power values of UAVs, the optimization unit in the cloud performs energy scheduling by sending the specific location coordinates and the communication unit's power value to the UAVs in the network.
UAV system
For the solar powered UAVs, the simple energy input/output model is used. As described in [3], this work considers the electrical energy
The total electrical power output
The payload power
The motor controller, gearbox, motor, and propeller efficiencies are comprised to get the
The
Lastly, the incoming solar power
Deep learning algorithm
As we need to predict the future harvested solar power values for energy optimization, a suitable Machine Learning (ML) algorithm must be modeled. Before modeling it, we studied several deep learning algorithms that could solve most of the time series forecasting problems. However, before going into deep learning, we tried some approaches like autoregression and moving average algorithms, although they were able to forecast the future solar power. Still, they could not be able to follow the pattern of the dataset, and also, the temperature, humidity, and weather data were not able to be embedded into it. Thereby, they developed a significant estimation error.
To involve the weather data and predict the solar power pattern, we moved to deep learning-based approaches. We used an algorithm called Recurrent Neural Networks (RNN). However, the vanishing gradient problem in RNN made the time series forecasting prone to training errors. The root cause of RNN is that it loses its memory over a period and makes the prediction only based on the previous input value rather than the sequence of inputs. Based on the RNN's feedback and results, we selected a memory-based deep learning algorithm called Long Short-Term Memory (LSTM) Neural Network. The LSTM Neural Network consists of several gates called input, forget, and output gates to accomplish the time series prediction. It replaces each hidden unit of RNN with a memory unit and adds a memory cell. As the gates control the memory units, it retains the previous information over a long period and helps solve the time series forecasting problems.
Poisson process
The distribution of users in the coverage region is estimated using the reference [23]. Then the power required for the communication unit is determined utilizing the arrival rate of the users
The probability of users count is found using Equation (8), where
Summary
The energy optimization algorithm block receives the estimated user's count, predicted solar power data, solar harvesting power, and the UAV energy consumption values. Finally, Utilizing these data points, the block outputs the required transmission power for the small cell. The block also computes the UAV flying time and battery energy. Likewise, utilizing future solar power value and user count, it communicates with other UAVs to perform energy scheduling to help the users in future periods. The algorithm's function and the UAV energy calculations are discussed in the problem formulation.
PROBLEM FORMULATION
In this section, we show the problem formulation for LSTM deep learning model, adaptive power consumption mechanism, and energy scheduling mechanism using multiple UAVs. Based on the number of users and predicted solar power, the UAV can adaptively change its communication unit's power and also performs multi-UAV-based communication.
LSTM modeling
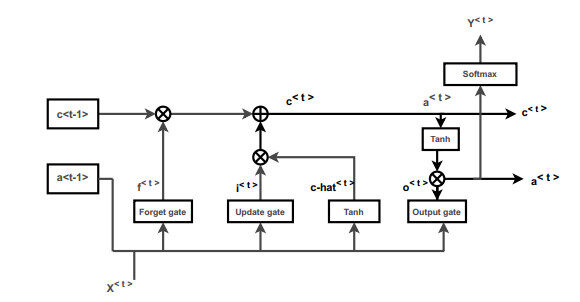
The LSTM Neural Network model has layers similar to recurrent neural networks, but it has an additional memory cell unit which propagates through all the layers by carrying out some information about the previous input sequence. From the reference [24], the Memory cell unit has several gates which make the LSTM more powerful than RNNs. These gates are explained below.
Figure 3 shows the block diagram of LSTM Neural Network, which begins with the input layer where
The
A toddler memory unit is introduced and its value is calculated using
Energy consumption and optimization model
For energy optimization, our proposed algorithm fetches the available energy in the battery
where
The power at the Electronic Speed Controller (ESC) can be determined using
where
Furthermore, the net power consumed from the battery can be found by taking the difference between the amounts of power drawn from the battery and the amount of solar power
The flying time of the UAV is calculated for every time slot, and it is found using Equation (17),
The main aim of this approach is to maximize the flying time of the UAVs by altering the communication unit's transmission power based on the number of ground users. From the optimization function in Equation (18), the power for communication unit
The inequality constraints of the optimization function are the transmission power of the communication unit, which is limited between 1-6 Watts, and the arrival rate for a particular region is less than or equal to 62 users. Based on the arrival rate of ground users, the optimization variable
Energy scheduling
As the future solar power is predicted using the LSTM model, the scheduling strategy is followed by future solar power
At last, the energy
SIMULATION AND RESULTS
As our requirement is to predict solar energy for the next time period, we first need to create a power dataset with the specific solar panel which is mounted over the UAV. The global horizontal irradiation data for 16 years from National renewable energy resources have been extracted for our location, and a specific formula has been devised to simulate the power produced from a single cell monocrystalline solar panel.
Change in efficiency Z is calculated using the T value which is the extracted temperature value of the specific Global Horizontal Irradiance (GHI) zone; change in temperature per degree decreases the panel efficiency by 0.32 percent. Then the solar power
Training the LSTM
The LSTM model, which is discussed in the problem formulation, is built using Keras library, and the processed data is split into training and test data sets. The training set data has 80 percent of the original data, which is converted to a sequence of data arrays of window size 48.
The prepared sequence data is fed into a point-by-point LSTM prediction model, which predicts only a single point ahead of each time sequence. The model has 48 input units followed by three hidden layers with a dropout rate of 0.05 and ends with a dense layer (output unit) to predict the value Y from the sequence of inputs. The gradient descent is performed using Adam optimizer and the performance of the system is calculated using Root Mean Square (RMS) approximation. Once the LSTM unit is constructed, Training data is fed into the model by setting the epoch rate and batch size. Eventually, the RMS value is monitored, and finally, the trained model is tested against the test data set to evaluate the performance of the model.
Performance analysis
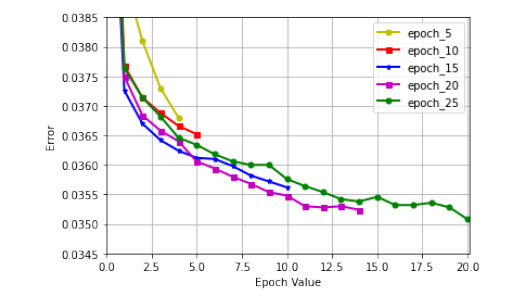
The LSTM model is initially trained with a batch size of 48 at an epoch rate of 5. Then gradually, the epoch rate is increased for various values like 10, 15, 20 and 25. Respective Root Mean Square Error is calculated for various epoch rates. Then the trained model is tested against the test data set, and the predicted values are plotted in a graph for different epoch values.
Figure 4 shows the output of RMS Error with respect to various epoch rates. With the increase in the epoch rates, i.e., from 5 to 25, the RMS Error values also decreased from 0.0370 to 0.0346, and beyond this epoch rate, the error became constant.
Figure 5 shows the gradient convergence value
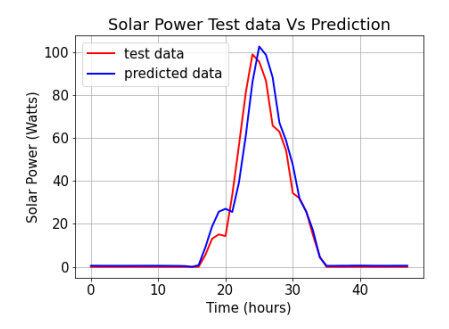
After the training, the LSTM model, which is trained at a 25 epoch rate, is saved, and the model's accuracy is tested with the test dataset. The Figure 6 shows the predicted result of the model, which is tested against the test dataset. The test dataset has the total power harvested by all the cells, i.e., 88 cells. The prediction shows that each UAV can harvest to a maximum of 101 W and a minimum of 0 W.
Implementation of algorithm and results
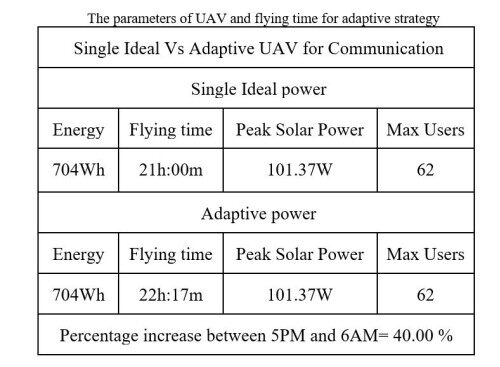
From the LSTM model, the solar values are predicted for a day and are stored in a list. The list consists of 48 values, and each represents the power output from the solar panel for every half an hour. The UAV parameters are utilized from reference [3], which has a battery energy of 704Wh and has 88 sun C60 solar cells in it. The power consumed by the UAV, the number of cells and the peak power harvested from each cell are shown in Table 1. The UAV has a high flying time based on the harvested solar power. So, using these parameters, a simulation model is built to determine the flying time and energy consumption from the battery bank. The transmission power value of the communication unit is set to 6 W for the ideal case and varied from 1-6 W for the adaptive case.
Simulation parameters
| Parameters for simulation | |
| Parameters of UAV | Value |
| Battery energy | 704Wh |
| Motor power | 59 W in day and 41W in night |
| No of solar cells | 88 |
| Power of a solar cell | 1.2W(at peak per cell) |
Based on the graph [23], the actual user count is found for each hour. Then using the Poisson process, the probability of user count is predicted. With the help of user count, the transmission power is determined. In the first stage, the whole system is made to consume the ideal power value, i.e., 6Watts for the communication by using the small cell [25], and the algorithm is simulated to determine the air time of the UAV, including the small cell power.
The simulation equation for determining the time and energy consumed by the UAV as follows,
The Equation (23), Equation (24), and Equation (25) are simulated over a period of
Energy scheduling is another important aspect where the system optimizes the power consumption using the future solar power and user arrival rate. If a case arrives that the users in the single small cell range are going to increase for the next time slot, fortunately, the UAV system predicts the future harvested solar power value and transmission power. Using the determined values, the system calculates the amount of energy that will be utilized for the next time period and their respective flying time. If the system is not sufficient to cover the entire users in its range and does not have enough energy to sustain for the next time period, it immediately sends a request to the nearest UAV to support its range for the next time period. Typically, the requested UAV would be getting a response from the nearest UAV for support; if in case the request has not been addressed, the UAV would be going into energy-saving mode until it stops supporting the users in its range. For example, if the number of users in a UAV range is going to increase from 60 to 120, then that UAV gets support from another to support the high users range by sharing the required transmission power. Thus, intercommunication between the UAV happens, and finally, the total energy is split by two UAVs to provide a wireless connection to the users. By doing this, the actual airtime of the UAV increases to an extent and the resources are also properly utilized.
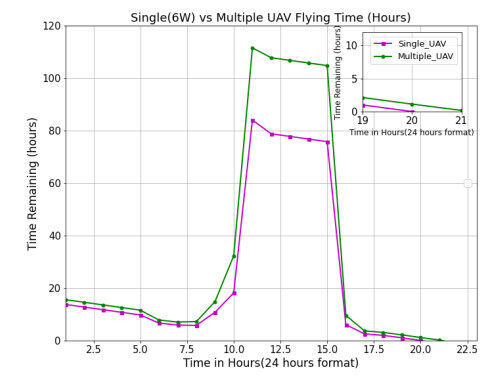
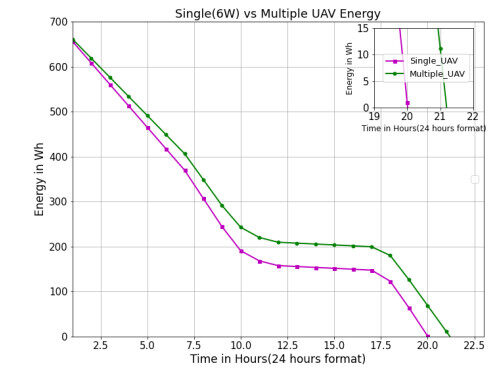
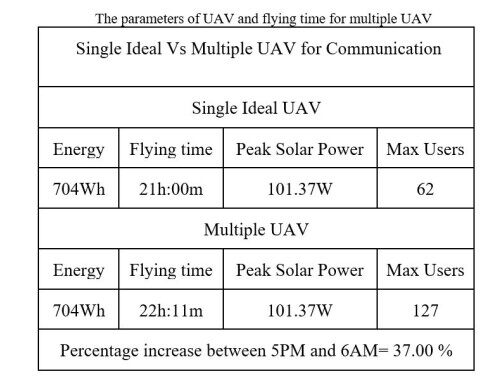
For simulation purposes, only two UAVs are considered for multiple UAV cases. Therefore, at a point in time, the energy in the ideal single UAV drops to zero, but the multiple UAV topology still has 70WHr energy to support the users.
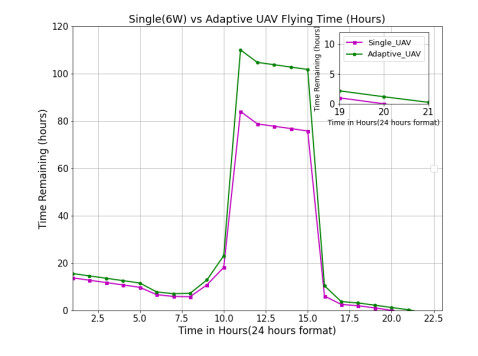
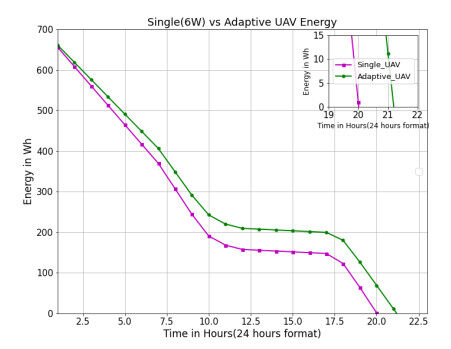
Figure 9 shows the difference in flight time due to the high number of users for a single ideal UAV and the multiple UAV topology. Figure 10 shows the energy that has been consumed by the ideal single UAV and multiple UAVs. The single UAV system can withstand only 21 hours, but the adaptive scheduled multiple UAVs can fly in air for up to 22 hours 11 minutes; the scheduling system has made the UAV fly for another 71 minutes in the air.
Figure 11 and Figure 12 indicates the energy in the batteries, peak solar power harvested by the UAVs and the maximum number of users in the range of the UAVs. The simulation results show that the adaptive and multiple UAVs have a significant increase of 40% and 37% in the flying time compared to the single ideal UAV configuration.
CONCLUSION
In this paper, we have modeled the system to support communication for the users in the SAGINs. We have focused more on the energy and resource management of the UAVs, which are used to provide communication in rural and network-constrained areas. The modeled system is placed on the solar powered UAV, which utilizes the harvested solar power from the Sunpower C60 panels. In order to optimally utilize the energy from the battery and to increase the flying time, first, the future solar power values are predicted using the LSTM model and the arrival rates of the users are calculated using the Poisson process. Then, these data are fed into a novel algorithm, which makes the system draw power for the communication adaptively and schedules the work by getting support from other UAVs to share the power during the larger user arrival rate. Battery, motor, and other parameters are evaluated. The algorithm is simulated to determine the flying time for various topologies, and finally, we achieved an increase of 40% in the flying time.
DECLARATIONS
Authors' contributions
Major contribution in doing the simulation and writing the paper: Ravi P
Revision of the manuscript: Wang M
Validation of results and Manuscript revision: Scott MJ, Wang M
All authors read and approved the final manuscript.
Availability of data and materials
Not applicable.
Financial support and sponsorship
None.
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2022.
REFERENCES
1. Liu J, Shi Y, Fadlullah ZM, Kato N. Space-air-ground integrated network: a survey. IEEE Commun Surv Tutorials 2018;20:2714-41.
2. Ghazzai H, Menouar H, Kadri A, Massoud Y. Future UAV-based ITS: a comprehensive scheduling framework. IEEE Access 2019;7:75678-95.
3. Oettershagen P, Melzer A, Mantel T, Rudin K, Stastny T, et al. Perpetual flight with a small solar-powered UAV: flight results, performance analysis and model validation. 2016 IEEE Aerospace Conference 2016:1-8.
4. Sekander S, Tabassum H, Hossain E. Statistical performance modeling of solar and wind-powered UAV communications. IEEE Trans on Mobile Comput 2021;20:2686-700.
5. Kato N, Fadlullah Z, Tang F, et al. Optimizing space-air-ground integrated networks by artificial intelligence. IEEE Wireless Commun 2019;26:140-47.
6. Wang Y, Xu Y, Zhang Y, Zhang P. Hybrid satellite-aerial-terrestrial networks in emergency scenarios: a survey. China Commun 2017;14:1-13.
7. Cheng N, Quan W, Shi W, et al. A comprehensive simulation platform for space-air-ground integrated network. IEEE Wireless Commun 2020;27:178-85.
8. Li Z, Wang Y, Liu M, et al. Energy efficient resource allocation for UAV-assisted space-air-ground Internet of remote things networks. IEEE Access 2019;7:145348-62.
9. Liu Q, Li M, Yang J, et al. Joint power and time allocation in energy harvesting of UAV operating system. Computer Communications 2020;150:811-7.
10. Morton S, D'Sa R, Papanikolopoulos N. Solar powered UAV: design and experiments. 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) 2015:2460-66.
11. Jashnani S, Nada T, Ishfaq M, Khamker A, Shaholia P. Sizing and preliminary hardware testing of solar powered UAV. Egypt J Remote Sens Space Sci 2013;16:189-98.
12. Oettershagen P, Melzer A, Mantel T, Rudin K, Lotz R, et al. A solar-powered hand-launchable UAV for low-altitude multi-day continuous flight. 2015 IEEE international conference on robotics and automation (ICRA) 2015:3986-93.
13. Turgut E, Cenk Gursoy M, Guvenc I. Energy harvesting in unmanned aerial vehicle networks with 3D antenna radiation patterns. IEEE Transactions on Green Commun Netw 2020;4:1149-64.
14. Cong J, Li B, Guo X, Zhang R. Energy management strategy based on deep Q-network in the solar-powered UAV communications system. 2021 IEEE International Conference on Communications Workshops (ICC Workshops) 2021:1-6.
15. Zhang J, Lou M, Xiang L, Hu L. Power cognition: enabling intelligent energy harvesting and resource allocation for solar-powered UAVs. Future Gener Comput Syst 2020;110:658-64.
16. Thanh PD, Hoan TNK, Giang HTH, Koo I. Cache-enabled data rate maximization for solar-powered UAV communication systems. Electronics 2020;9:1961.
17. Manzoor A, Kim K, Pandey SR, et al. Ruin theory for energy-efficient resource allocation in uav-assisted cellular networks. IEEE Trans Commun 2021;69:3943-56.
18. Sun Y, Xu D, Ng DWK, Dai L, Schober R. Optimal 3D-trajectory design and resource allocation for solar-powered UAV communication systems. IEEE Trans Commun 2019;67:4281-98.
19. Sun Y, Ng DWK, Xu D, Dai L, Schober R. Resource allocation for solar powered UAV communication systems. 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC) 2018:1-5.
20. Last G, Penrose M. Lectures on the poisson process. Cambridge University Press; 2017;7.
21. Drela M, Youngren H. Xfoil 6.9 user primer. Department of aeronautics and astronautics, massachusetts institute of technology, cambridge, MA 2001;1.
22. National Renewable Energy laboratory. Available from: https://www.nrel.gov/ [Last accessed on 25 Aug 2022].
23. Heuser R. The data says: mobile traffic by day and time; 2015. Available from: https://www.seoclarity.net/blog/mobile-seo-by-day-and-time-11890/ [Last accessed on 25 Aug 2022].
24. Cui S. Solar energy prediction and task scheduling for wireless sensor nodes based on long short term memory. J Phys: Conf Ser 2018 1074:012100.
25. GSMA small cell deployment booklet. Available from: https://www.gsma.com/publicpolicy/wp-content/uploads/2016/12/GSMA_Small_Cell_Deployment_Booklet.pdf [Last accessed on 25 Aug 2022].
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Ravi P, Wang M, Scott MJ. Solar powered UAV charging strategy design by machine learning. J Smart Environ Green Comput 2022;2:126-42. http://dx.doi.org/10.20517/jsegc.2022.02
AMA Style
Ravi P, Wang M, Scott MJ. Solar powered UAV charging strategy design by machine learning. Journal of Smart Environments and Green Computing. 2022; 2(3): 126-42. http://dx.doi.org/10.20517/jsegc.2022.02
Chicago/Turabian Style
Ravi, Prakash, Miao Wang, Mark J Scott. 2022. "Solar powered UAV charging strategy design by machine learning" Journal of Smart Environments and Green Computing. 2, no.3: 126-42. http://dx.doi.org/10.20517/jsegc.2022.02
ACS Style
Ravi, P.; Wang M.; Scott MJ. Solar powered UAV charging strategy design by machine learning. . J. Smart. Environ. Green. Comput. 2022, 2, 126-42. http://dx.doi.org/10.20517/jsegc.2022.02
About This Article
Copyright
Data & Comments
Data
 Cite This Article 10 clicks
Cite This Article 10 clicks














Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.