UAV assisted communication for ground users using machine learning and optimization
Abstract
Aim: Among a large number of products that support communication, there is one called space air ground integrated networks (SAGIN's), which is the most commonly used to support users in rural and emergency situations. Typicaly in emergency situations SAGIN's use unmanned aerial vehicles (UAVs) in their air layer to temporarily support the ground users. Although the cost of UAVs is lower than that of traditional base stations, and their actions are more flexible, but their battery life problems lead to frequent charging of drones, resulting in many resource losses and unable to provide communication support. In order to mitigate the issues, novel optimization algorithms need to be developed to support the ground users.
Methods: In this work, we develop a grid-based deep learning method using the LSTM model to estimate the number of ground users as vehicles in each area, and developed an optimization algorithm to minimize the number of UAVs needed to the user's and meanwhile to satisfy quality of service (QoS) requirements. For optimization, we mainly use the Linear Optimization Tools and an objective function has been developed using density predicted and SINR data to achieve acceptable QoS.
Results: The simulation results shows that this approach has improved the quality of the communication by 50%.
Conclusion: Using unique grid technique and the LSTM machine learning model, the user densities on each partitioned grid is determined. Finally, a linear optimization algorithm is developed based on the user density to determine the lowest number of UAVs to support the users in each grid while maintaining the QoS.
Keywords
INTRODUCTION
The space air-ground integrated networks (SAGINs) are emerging to give extensive area coverage, high throughput, and high transmission to ground users in the future generation wireless networks as in article[1].They also used to expand the communication coverage range and enhance network capacity. Three main layers make up SAGINs: a space layer, a ground layer, and an air section. Satellites in the space layer enable seamless connectivity, and the terrestrial network enables high-speed communication. UAVs and/or balloons make up the air segment, which is crucial for supplying broadband wireless connectivity to support the terrestrial networks. Numerous benefits, including improved connection and support for future 5G communications at high data rates, would result from the combination of these network layers. In the air layer, especially the UAVs provide users with a fast and reliable connection at a lower cost and with less complexity than the static base stations used in terrestrial networks.
UAVs have comprehensive and specific applications in modern society. In daily life, in intelligent environments, UAVs can use intelligence edge platform to collect data to undertake the function of relay station cited in [1], and are often used as mobile base station to monitor specific areas and provide services as in paper [2]. In disasters, drones shoulder the important functions of evacuating crowds, guiding escape, and helping rescue in paper [3]. Especially in cases where intelligent communication systems are destroyed, report shows that UAVs can help SAR (synthetic aperture radar), which plays an essential role in guidance of disaster affected people, to obtain critical emergency data in paper [4]. In factories, drones have played a huge role in realizing the important safe collaboration between machines in Industry 4.0 as shown in paper [5]. In multiple interactive networks, including B5G (beyond fifth generation) wireless interactive network and IoT (internet of things), drones have been proven to have the ability to provide data in a timely manner in paper [6]. In many of the above fields, UAVs have significant advantages over fixed base stations, especially in terms of mobility, agility, and degrees of freedom in paper [7]. However, there has not been a big breakthrough in the energy endurance of UAVs in recent years shown in paper [1, 8]. Faced with the contradiction between cost and service quality, we must think of new balance methods. In paper [8], researchers tried to solve the problem by balancing power consumption and transmission distance. In spite of the fact that the solar powered UAVs are extensively supporting the ground users for a longer duration of time, the allocation of UAVs to particular ground user regions is also an essential factor that deals with saving the energy of the UAV. The graph in paper [9] shows the density of devices that is turned on during a particular day, and that data can be used to find the active users count. The only concern with the information is that it doesn't provide the specific region where the devices are involved, and the rate of change in users count is not frequent. Therefore, an appropriate count of ground users needs to be found to allocate the UAV properly. A novel approach has been developed in this paper by utilizing the Beijing downtown vehicle location dataset from article [10], and [11]. It consists of vehicle latitude and longitude data for every minute for seven days. From the dataset, the total area of the region is found, and its split into several grids. The number of users in each grid is found using the novel grid density algorithm, and the future girds densities are forecasted using LSTM neural networks as shown in paper [12]. Finally, an optimization algorithm has been developed using Linear optimization tools in article [13, 14] and an objective function has been devised using UAV, density, and SINR as in paper [15]. With the help of inequality constraints and optimization variables, the function is iterated over density data to determine the number of UAVs to support the grids by satisfying the adequate QoS. The remainder of the paper discusses the related works and system model in Section Ⅱ and Section Ⅲ. Illustration the problem formulation in Section Ⅳ. Section Ⅴ shows the simulation and the respective results. Finally, the paper ends with the conclusion and references.
RELATED WORKS
Numerous studies have been conducted to enhance mobile users' communication in rural and disaster-affected areas. The author claims in paper [16] that SAGINs are currently frequently used. Most significantly, SAGIN air networks are crucial to provide wireless connectivity to users as base stations might become overloaded in a major disaster area. The author of paper [17] claims that in order to give ground users fast data rates and reliable communication, it is required to construct an emergency network employing UAVs. According to article [17], the controllers are deployed in the simulation-based SAGINs to improve network operations and deliver effective quality of service (QoS) to customers. These works don't have any information on how energy is optimized to allow UAVs to fly for longer periods of time. As the air layer in SAGINs are playing a predominant role in providing connectivity, therefore the UAVs are used by the communication community to support the ground users. In order to offer wireless connectivity in the required locations, UAVs are designed to carry communication units like small cells paper [18]. According to the author in paper [19], power allocation and trajectory design issues in multi-UAV based communication systems are resolved utilizing machine learning. By resolving trajectory design issues, the successive convex approximation approach described in paper [20] and [21], makes it possible to communicate with ground users and increases the system's overall throughput. Although some study has been done to improve the users' ability to communicate, the density of the ground users have not been taken into account. Additionally, the UAVs aren't effectively distributed based on user requirements. Having an ideal communication system also requires proper UAV allocation in the necessary areas and the lowering of message delay. According to article [22], there is a lot of traffic on the Vehicle to Everything (V2X) network in urban areas. As a result, there is a delay in the communications that the cars transmit and receive. Unexpected traffic growth on the V2X will cause a delay in the delivery of emergency alerts. Due to the high volume of traffic in urban areas, the crowd flash happens. The author of paper [23] has succeeded in resolving this issue by doing a few things. First, by utilizing a graph convolution network to forecast traffic volumes, and then, by giving priority to transmit packets for the V2X communication network. This might also be overcome by using drone cells to reduce traffic congestion in Road Side Units, in agreement to paper [22]. According to article [24], the spatio-temporal trajectories are utilized to estimate the vehicle density, and the predicted data is then used to determine the optimal path for transmitting data packets to the preferred destination. As per article [25], the density prediction is also utilized in vehicular Ad-hoc networks (VANETs) to create an intelligent routing system for sending and receiving packets and assessing the performance of communication methods. Several optimization methods are implemented to increase energy efficiency, for instance, in paper [26] and [27] the author used optimization techniques and an iterative process to solve an energy efficiency maximization problem. In article [28], a convex optimization is employed to maximize the uplink and downlink data packets while full duplex small cell UAVs are utilized to support the connection. The performance of the algorithm is compared to brute force methods, and a sub-optimal solutions are discovered. These studies made it clear that the traffic density data and optimization techniques are reliable and useful for planning methods in beforehand. The previous studies also used the density prediction data to route data packet, whereas they did not use real time density data with optimization techniques to employ flying base stations in emergency situations.
A comparison of the related works mentioned in this section is included in Table 1.
Comparison among the related works
| Reference number | Scenario | Main method |
| [16] | Space Air Ground Integrated Networks (SAGINs) | Artificial Intelligence (AI) |
| [17] | Low altitude platforms (LAPs) | Hybrid satellite-aerial terrestrial (HSAT) networks |
| [19] | Unmanned aerial vehicle (UAV) networks | Swarm optimization |
| [20] | Unmanned aerial vehicle (UAV) networks | Monotonic optimization |
| [21] | Multicarrier (MC) systems | Suboptimal algorithm |
| [22] | Intelligent Transportation System (ITS) | Topological Graph Convolutional Network (ToGCN) |
| [23] | Radio access network (RAN) | Proactive drone cell deployment framework |
| [24] | Internet of Things (IoTs) | Collaborative communication scheme |
| [25] | Vehicular ad hoc networks (VANETs) | Intelligent prediction based routing algorithms |
| [26] | unmanned aerial vehicle (UAV) networks | Energy efficiency (EE) maximization scheme |
| [27] | UAV enabled wireless communications | Efficient iterative algorithm |
| [28] | Unmanned aerial vehicle (UAV) networks | Block coordinate descent method |
SYSTEM MODEL
Vehicle representation
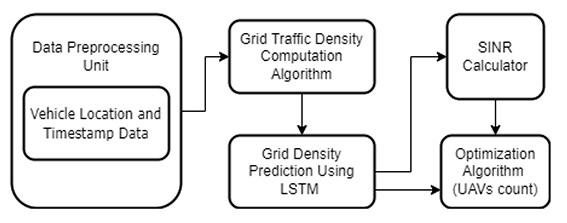
The system model depicted in Figure 1 is divided into three distinct blocks. The first is the data pre-processing, where vehicle location and timestamp information are taken from the Beijing vehicle location dataset in paper [10], and [11]. Each location data point that falls within the chosen area
The second block consist of density computation and prediction part, which uses the data from the preceding unit. The traffic density estimation algorithm is then used to calculate the vehicle count. The region
In the second block, the grid density prediction algorithm, which is built with LSTM neural networks, takes in each grid data
The final block, known as the optimization block, includes the average number of data packets that each vehicle will transmit as well as the real capacity,
Grid-based density algorithm
The second block in the system model is the algorithm block where the data from the previous unit is taken and the vehicles count in each and region is calculated using the traffic grid density computation algorithm as shown in Figure 1. Where the region
Linear optimization
As shown in Figure 1, the last block is the optimization part where using the vehicles density data in each grid, the Signal to Interference Noise Ratio (SINR) is calculated for each region and that is sent to the optimization algorithm to determine minimum number of UAVs required to support the ground vehicle users, in which the UAVs and the SINR data are the optimization variables used in the function and with the help of linear optimization tools, the required amount of UAVs to support the users in each grid is found.
LSTM modeling
A recurrent neural network-based algorithm called long short-term memory (LSTM algorithm) as in paper [12] is applied to obtain the vehicles' anticipated latitude and longitude coordinates. The mentioned algorithm has advantages in compensation for the vanishing gradient problem, which is apparent in recurrent neural networks. The input layer of the LSTM model would take in the location data in the past, e.g.,
A toddler memory unit is also introduced in the hidden layer, and its value is determined through the hyperbolic tangent
PROBLEM FORMULATION
Traffic density analysis
An algorithm is designed as in Algorithm 1 to predict each grid's density value at time reference
Algorithm 1 grid density algorithm 1: procedure getDensity(
2: for
3:
4:
5: for
6:
7:
8:
9: while curLat not in latn do
10:
11: if
12: break
13: end if
14: end while
15:
16: while curLon not in lonn do
17:
18: if
19: break
20: end if
21: end while
22: if
23:
24: end if
25: end for
26: end for
27: end procedure
In the algorithm, the system scans through each vehicle, e.g.,
The resulting traffic density data is recorded as shown in Figure??, where
Linear optimization
Linear programming (LP) optimization is a method for the optimization of objective function, dependent upon equality or inequality constraints. It is used in various fields of engineering to make the process cost effective and efficient. Currently they are used in energy, manufacturing and engineering sectors. There are several tools and libraries available to solve the LP problem. In this work PULP as in article [29] a python based library is used to model the objective function. The Equation 4.4 has the objective function
Quality of service requirements
This work aims not only to find the required number of UAVs but also to satisfy the quality of service requirements (QoS requirements. The QoS considered here is to maximize the throughput for the uplink scenario, i.e., to receive the data packets transmitted from the ground vehicles. Since the data packet size is very small, an ideal MAC layer is considered for this scenario. The QoS is determined using the probability of successfully transmitting data packets over a channel to the UAVs, as the SINR and channel capacity are the resources that significantly influence the transmission's performance. Therefore, the system is simulated in this work by including the SINR and the channel capacity as QoS parameters.
Optimization algorithm
The whole system aims to find the minimum number of UAVs to support the vehicles in each grid based on the supply and demands. Linear optimization is considered from paper [13] is used to develop a cost function for the problem. First, the UAV (
The cost function holds an objective variable,
Optimization variables are initialized to lower bound values and they are made to be subjected to
SIMULATION RESULTS
Problem setting
This project is based on data from Taxi Software's published trace files in China as in paper [10] with over ten thousands trace files. Each row of the trace file would record the driver's identification number, the date and time reference of the row, the Longitude, and the Latitude. An row demonstration for taxi driver with id 9862 is listed in table 2
Row Demonstration for Taxi Driver with ID 9862
| 9862 | 2008-02-02 | 13:37:28 | 116.39389 | 39.8693 |
| 9862 | 2008-02-02 | 13:42:30 | 116.36976 | 39.86971 |
| 9862 | 2008-02-02 | 13:47:32 | 116.37988 | 39.86918 |
| 9862 | 2008-02-02 | 13:52:34 | 116.38953 | 39.85745 |
For accuracy and convenience of grid prediction, this study eliminates repeating data points, applies a consistent interval approach as in article [30], and transfers the time reference from date and time into timestamps. Also, to balance the need for location accuracy and sufficient amounts of vehicle for prediction, the calculated is proceed in the center part of Beijing. The map is divided into 20 by 20 grids that are about 1.6km by 1.3 km.
Grid data analysis
With more than 10, 000 drivers' trace files, it was plausible to create a density map to describe the density characteristics in each grid. We defined the time-dependent grid density as the number of vehicles in it given a specific time.
Map setting-up
We defined grid density by how many vehicles were in the specified grid at a given time reference. Initially, the map is divided into three by three grids and simulated each grid's density. The attempt was successful, but a couple of flaws appeared when we took a closer look. The most profound problem was that the grid was too big for any meaningful applications. Note that the original map is the Beijing City with about 6336 square miles. That means each grid was about 704 square miles. Thus, when considering the application of resource allocation, it was barely possible for a vehicle to travel from one grid to another without using up all the energy. Also, most taxi drivers would only travel within a single grid most of the time, making path planning meaningless. To choose the most appropriate portion of the map, we first observed the density in each grid. Then, we could see that the middle grid has the highest density. Furthermore, we were noted that about 70 percent of all the available vehicles are in the central area most of the time. Also, due to the traffic prosperous of the central city, we could make an essential assumption that this part of the map was fully connected. Thus, we decided to use only the middle grid as our map. One essential part of path-planning was to narrow down the area of each grid so that the prediction could be more precise. Therefore, we decided to divide the map into 20 by 20 grids, where each grid would have about 1.6 km (latitude) by 1.3 km (longitude). In this way, we could build a map detailed enough for path planning.
Vehicle setting-up
First of all, we needed a vehicle that traveled across the map we chose, Beijing's central region. We selected all the taxis that satisfied one of the following criteria:
(ⅰ) it touches both the higher and lower latitude boundaries.
(ⅱ) it touches both the higher and lower longitude boundaries After filtering, we had about three hundred vehicles that satisfied the criteria. Besides the traveling range, we also wanted the selected vehicle to stay on the map as long as possible. We tried to select any vehicle that spent more than 99 percent of the time in the central region. And this requirement helped us narrow the candidates into 12 cars. We wanted the vehicle to have a longer time on record to better train the driver's preference model. Thus, we selected the car with the most prolonged duration on record, with identification number 9318. It had 8882 minutes of data on record.
Traffic density model prediction and results
We iterated through each driver's trace file and found the corresponding gird for each moment in our approach. If the vehicle were in the map chosen, we would increment the density in the landed grid. After going through all trace files, we gathered the density.
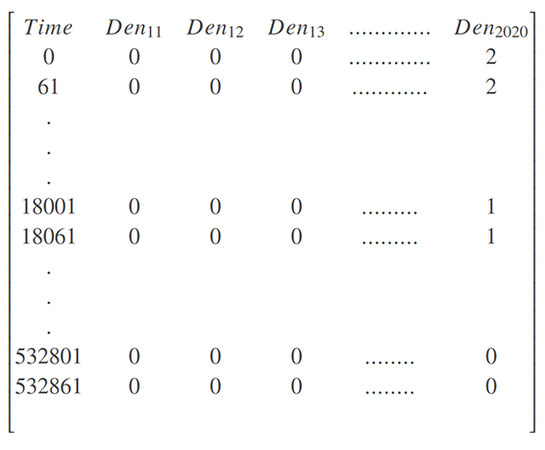
First, we needed to extract the data required for the grid's simulation and prediction from each driver. So we created a density file with 8882 minutes in length and four hundred grids in width. We then scanned through each driver's file and checked for the area it stayed at each reference. We then find the corresponding time reference and the grid of the vehicle's location in the density file and add one to the density number. Thus, after scanning through all the driver's data files, we successfully extracted the density file we desired. A preview of the desired file is shown in Table 3:
Preview of density file
| Time | A_1, 1 | A_1, 2 | A_1, 3 | ...... | A_2, 1 | A_2, 2 | A_2, 3 | ...... | A_20, 18 | A_20, 19 | A_20, 20 |
| 0 | 0 | 0 | 0 | ...... | 0 | 0 | 0 | ...... | 0 | 2 | 2 |
| 61 | 0 | 0 | 0 | ...... | 0 | 0 | 0 | ...... | 0 | 3 | 2 |
| ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... |
| 18001 | 0 | 0 | 0 | ...... | 0 | 0 | 0 | ...... | 4 | 2 | 1 |
| 18061 | 0 | 0 | 0 | ...... | 0 | 0 | 0 | ...... | 4 | 2 | 1 |
| ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... |
| 532801 | 0 | 0 | 0 | ...... | 1 | 0 | 0 | ...... | 0 | 0 | 0 |
| 532861 | 0 | 0 | 0 | ...... | 0 | 0 | 0 | ...... | 0 | 0 | 0 |
After having the grid's density data for each time reference, we could train each grid individually using LSTM models. We utilized an LSTM model with two layers with n units, a dropout of 0.05, and a dense layer with one unit. We used three epochs and a batch size of thirty while fitting. For accuracy, we could see that using the same model for all four hundred grids is a challenge, while it was not practical to form four hundred different models. One approach is to normalize all the processing data into the desired range. Since the model described above performs better when predicting series about five, we built the normalization this way:
In the above equation,
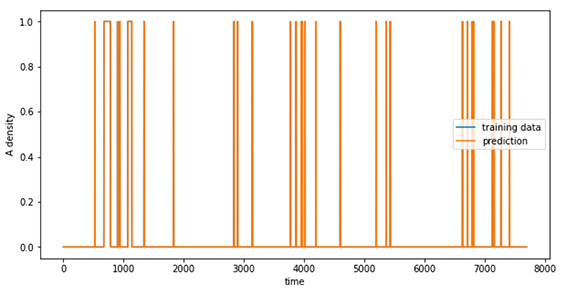
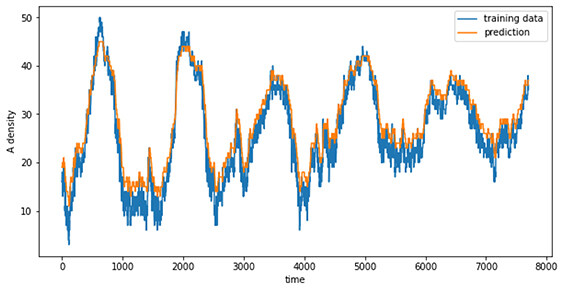
We see this model would successfully capture the character of a lower density grid. A graph representing the training data and the prediction for density value up to ten is as shown in Figure 4.
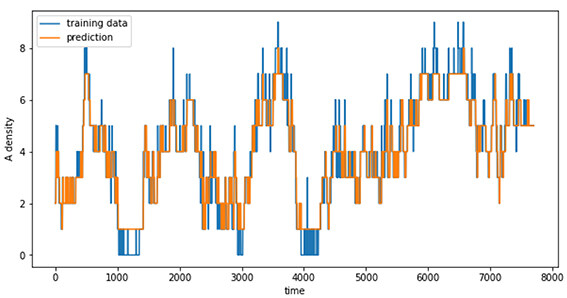
Again, the models gave an acceptable range of density that is accurate enough in comparing densities during path planning. A graph representing the training data and the prediction for density value up to thirty is as shown in Figure 5
The models gave an acceptable range of density that was accurate enough in comparing densities during path planning. Throughout all the grids, almost all of the densities were below sixty, and the above three situations should be representative enough to prove the accuracy of our models.
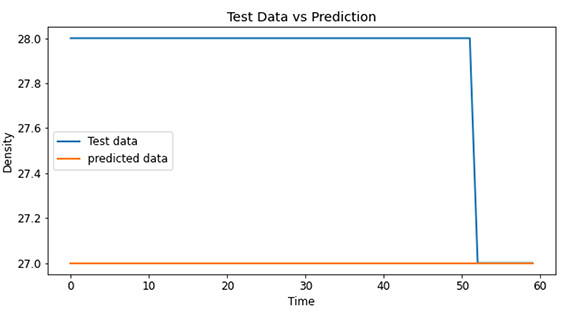
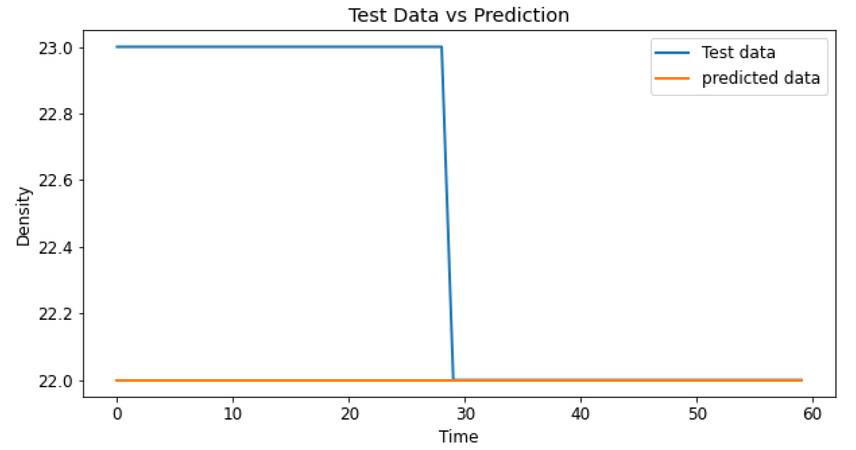
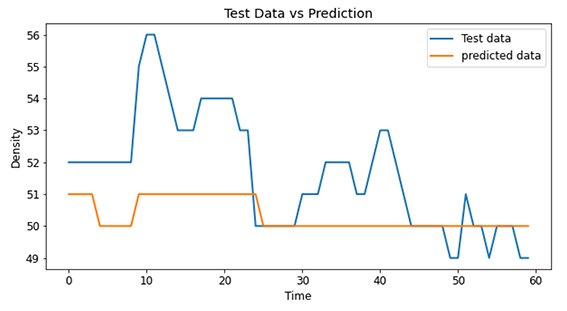
After modeling for all the grids, we tested the validations and their root-mean-square-error for each model. We could see that all the root-mean-square-error are less than one, meaning that the density difference between reality and prediction is less than one vehicle per grid in each minute, which was acceptable for our path planning. Demonstrations of the testing results are included in Figures. 6, 7, and 8.
Optimization results
After getting appropriate traffic density values in each grid, the optimization algorithm elaborated in the problem formulation is obtained to find the number of UAVs allocated for each grid. For that, the traffic grid density data is collected, and the SINR is chosen as the Quality of Service Parameter. The grid is nothing but the area that is chosen during map processing, where the beijing downtown has been subdivided into smaller regions (grids). Based on the vehicle count in each grid, the UAVs to support them are found.
The simulation part of the system uses the input density data
Input values for simulation
| Simulation parameter values | |
| Optimization parameters | Values |
| 0.5-1 | |
| Capacity | 30 |
| Transmission power | 1 W |
| 1 (data packet per vehicle) | |
Two inequality constraints in 9 are included in the optimization problem, and the optimization function should satisfy them. The cost function and optimization variables
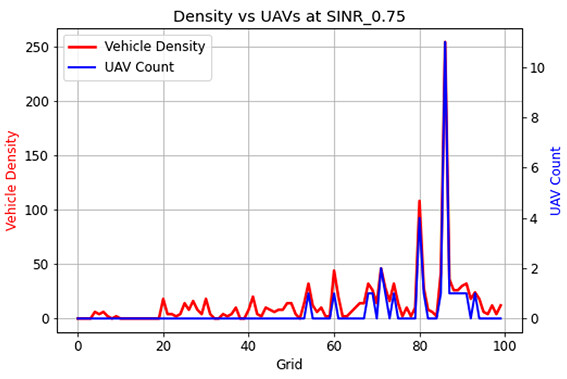
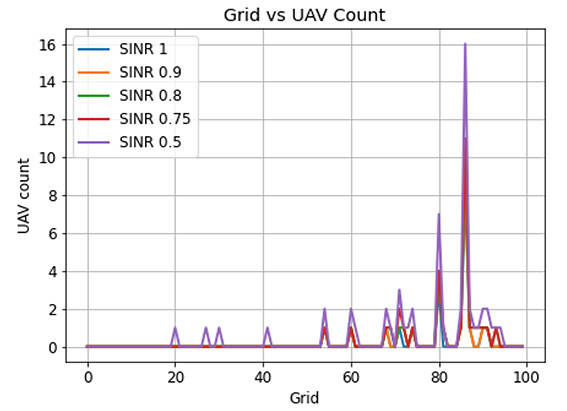
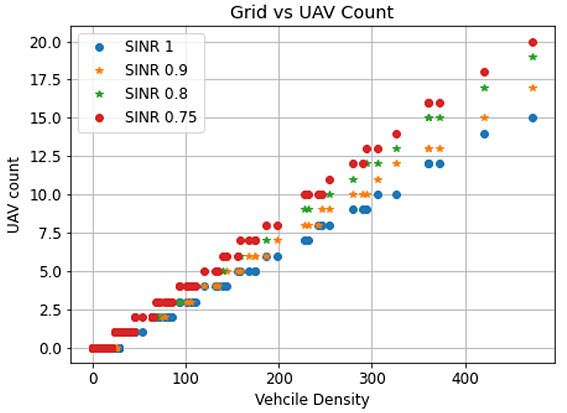
After the first set of simulations, Figure. 9 shows the users' density in each grid and associated UAVs for it. Based on the QoS parameter, i.e., at SINR 0.75 and the quantity of users in each grid, the UAVs are pushed through optimization to support the ground users. The graph also shows that UAV count is incremented whenever the users count reaches or exceeds the capacity of the communication unit. Figure 10 shows the result of UAVs for each grid concerning different SINR values. Basically, it depicts how the UAV count varies based on different SINR values. When the interference increases the count of UAVs are also increased regardless of the users count. To give a detailed picture, Figure 11 shows the count of UAVs with respect to the vehicle densities and different SINR values.
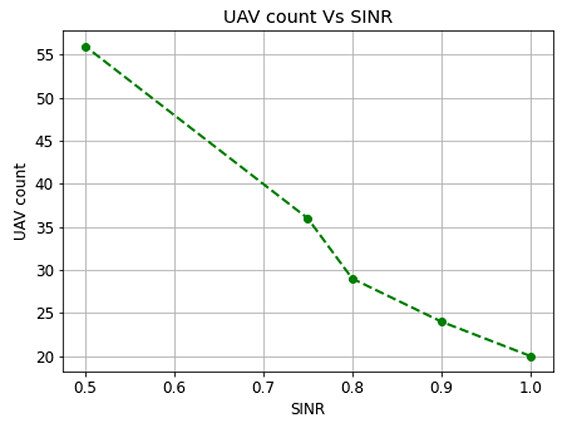
From Figure 12, a minimum of 20 UAVs are required to support a region when SINR is high. At the same time, when SINR becomes low, extra UAVs are pushed to maintain the QoS requirements. As a result, the UAV count becomes 32 to support the same users. The results show that the optimization algorithm finds the minimum number of UAVs by maintaining the QoS and thus it improves the quality of the connection by 50% to support the users.
DISCUSSION
The UAV-assisted communication advantages are discussed in this work, and the drawbacks of active user data have been studied. The ground users data has been utilized from the vehicle location dataset of Beijing downtown. The whole region is split into smaller grids using a grid partitioning algorithm to get the user density of each grid. The future density data are forecasted using LSTM neural network algorithm. Finally, a linear optimization algorithm is devised based on the grid density data to find the minimum number of UAVs to support the users in each grid by maintaining the QoS requirements. The simulations results show the number of UAVs that have been found for different QoS requirements.In the future works, noise and interference values can be directly measured and used in optimization rather than simulating the SINR values. Furthermore, the trajectories of the UAVs can also be optimized for better energy saving. Additionally, during optimization, outside environmental variables like wind and weather can be incorporated into the model to take real-world behaviors into account.
DECLARATIONS
Authors' contributions
Major contributions in doing the simulation and writing the paper: Ravi P, Zang T
Revision of the manuscript: Wang M
Validation of results and Manuscript revision: Scott MJ, Wang M
All authors read and approved the final manuscript.
Availability of data and materials
Not applicable.
Financial support and sponsorship
None.
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2022.
REFERENCES
1. Alsamhi SH, Almalki FA, Afghah F, et al. Drones' edge intelligence over smart environments in B5G: blockchain and federated learning synergy. IEEE Trans on Green Commun Netw 2022;6:295-312.
2. Saif A, Dimyati K, Noordin KA, et al. UAV and relay cooperation based on RSS for extending smart environments coverage area in B5G. Res Square 2022; doi: 10.21203/rs.3.rs-2002265/v1.
3. Alsamhi SH, Almalki FA, AL-Dois H, et al. Multi-drone Edge Intelligence and SAR smart wearable devices for emergency communication. Wirel Commun Mob Comput 2021;2021:1-12.
4. Alsamhi SH, Shvetsov AV, Kumar S, et al. UAV computing-assisted search and rescue mission framework for disaster and harsh environment mitigation. Drones 2022;6:154.
5. Alsamhi SH, Shvetsov AV, Shvetsova SV, et al. Blockchain-empowered security and energy efficiency of drone swarm consensus for environment exploration. IEEE Trans on Green Commun Netw 2022:1.
6. Alsamhi SH, Shvetsov AV, Kumar S, et al. Computing in the sky: a survey on intelligent ubiquitous computing for UAV-assisted 6G Networks and industry 4.0/5.0. Drones 2022;6:177.
7. Gopi SP, Magarini M, Alsamhi SH, Shvetsov AV. Machine learning-assisted adaptive modulation for optimized drone-user communication in B5G. Drones 2021;5:128.
8. Saif A, Dimyati K, Noordin KA, et al. Energy-efficient tethered UAV deployment in B5G for smart environments and disaster recovery. In: 2021 1st International Conference on Emerging Smart Technologies and Applications (eSmarTA). IEEE; 2021. pp. 1–5.
9. Heuser R. The data says: mobile traffic by day and time; 2015. Accessed: 2022-09-30. Available from: https://www.seoclarity.net/blog/mobile-seo-by-day-and-time-11890/. [Last accessed on 31 Dec 2022].
10. KDD '11: Proceedings of the 17th ACM SIGKDD international conference on Knowledge discovery and data mining. New York, NY, USA: Association for Computing Machinery; 2011.
11. Xin L, Wang P, Chan CY, et al. Intention-aware long horizon trajectory prediction of surrounding vehicles using dual LSTM networks. In: 2018 21st International Conference on Intelligent Transportation Systems (ITSC). Maui, Hawaii, USA; 2018. pp. 1441–46.
12. Yu Y, Si X, Hu C, Zhang J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Computation 2019;31:1235-70.
13. Bertsimas D, Tsitsiklis JN. Introduction to linear optimization. vol. 6. Athena Scientific Belmont, MA; 1997. Available from: https://linux.ime.usp.br/~dfrever/programs/Documents/INTRODUCTION%20TO%20LINEAR%20OPTIMIZATION(errata).pdf. [Last accessed on 31 Dec 2022].
14. Pirnay H, López-Negrete R, Biegler LT. Optimal sensitivity based on IPOPT. Math Prog Comp 2012;4:307-31.
15. Jo HS, Sang YJ, Xia P, Andrews JG. Heterogeneous cellular networks with flexible cell association: A comprehensive downlink SINR analysis. IEEE Trans Wireless Commun 2012;11:3484-95.
16. Kato N, Fadlullah Z, Tang F, et al. Optimizing space-air-ground integrated networks by artificial intelligence. IEEE Wireless Commun 2019;26:140-7.
17. Wang Y, Xu Y, Zhang Y, Zhang P. Hybrid satellite-aerial-terrestrial networks in emergency scenarios: a survey. China Commun 2017;14:1-13.
18. Zola A, Lewis S. What is a small cell? - definition from techtarget. com. TechTarget; 2022. Accessed: 2022-09-30. Available from: https://www.techtarget.com/searchnetworking/definition/small-cell. [Last accessed on 31 Dec 2022].
19. Chang Z, Guo W, Guo X, Ristaniemi T. Machine learning-based resource allocation for multi-UAV communications system. In: 2020 IEEE International Conference on Communications Workshops (ICC Workshops). IEEE; 2020. pp. 1–6.
20. Sun Y, Xu D, Ng DWK, Dai L, Schober R. Optimal 3D-trajectory design and resource allocation for solar-powered UAV communication systems. IEEE Trans Commun 2019;67:4281-98.
21. Sun Y, Ng DWK, Xu D, Dai L, Schober R. Resource allocation for solar powered UAV communication systems. In: 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC). IEEE; 2018. pp. 1–5.
22. Qiu H, Zheng Q, Msahli M, et al. Topological Graph Convolutional Network-Based Urban Traffic Flow and Density Prediction. IEEE Trans Intell Transport Syst 2021;22:4560-9.
23. Yang P, Cao X, Yin C, et al. Proactive Drone-Cell Deployment: Overload Relief for a Cellular Network Under Flash Crowd Traffic. IEEE Trans Intell Transport Syst 2017;18:2877-92.
24. Liu B, Sheng Y, Shao X, Ji Y. A Grid and Vehicle Density Prediction-Based Communication Scheme in Large-scale Urban Environments. In: 2021 International Conference on Information and Communication Technologies for Disaster Management (ICT-DM); 2021. pp. 22–25.
25. Jabbarpour MR, Malakooti H, Taheri M, Noor RM. The comparative analysis of velocity and density in VANET using prediction-based intelligent routing algorithms. In: Second International Conference on Future Generation Communication Technologies (FGCT 2013);2013. pp. 54–58.
26. Liu C, Feng W, Wang J, Chen Y, Ge N. Aerial Small Cells Using Coordinated Multiple UAVs: An Energy Efficiency Optimization Perspective. IEEE Access 2019;7:122838-48.
27. Zhang G, Yan H, Zeng Y, Cui M, Liu Y. Trajectory Optimization and Power Allocation for Multi-Hop UAV Relaying Communications. IEEE Access 2018;6:48566-76.
28. Hua M, Yang L, Pan C, Nallanathan A. Throughput Maximization for Full-Duplex UAV Aided Small Cell Wireless Systems. IEEE Wireless Commun Lett 2020;9:475-9.
29. Pulp. Accessed: 2022-09-30. Available from: https://pypi.org/project/PuLP/. [Last accessed on 31 Dec 2022].
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Ravi P, Zang T, Scott M, Wang M. UAV assisted communication for ground users using machine learning and optimization. J Smart Environ Green Comput 2022;2:175-91. http://dx.doi.org/10.20517/jsegc.2022.05
AMA Style
Ravi P, Zang T, Scott M, Wang M. UAV assisted communication for ground users using machine learning and optimization. Journal of Smart Environments and Green Computing. 2022; 2(4): 175-91. http://dx.doi.org/10.20517/jsegc.2022.05
Chicago/Turabian Style
Ravi, Prakash, Tianyue Zang, Mark Scott, Miao Wang. 2022. "UAV assisted communication for ground users using machine learning and optimization" Journal of Smart Environments and Green Computing. 2, no.4: 175-91. http://dx.doi.org/10.20517/jsegc.2022.05
ACS Style
Ravi, P.; Zang T.; Scott M.; Wang M. UAV assisted communication for ground users using machine learning and optimization. . J. Smart. Environ. Green. Comput. 2022, 2, 175-91. http://dx.doi.org/10.20517/jsegc.2022.05
About This Article
Copyright
Data & Comments
Data

 Cite This Article 7 clicks
Cite This Article 7 clicks












Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.